I thought more about the last question I added into the addendum of the Numberphile, Graph theory and Mathematica post
It can be succinctly stated as:
such that
and
.
In words:
For all integers m, greater than 19, there are two other distinct positive integers less than m such that the sum of each with m, when square rooted is an integer.
What is the shortest proof you can find for this statement?
I’ll give it a shot:
To cheat a bit and simplify the argument, assume that we have verified the cases up to and including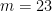 . By direct calculation
. By direct calculation
(this is true for and so true for all
and so true for all  ). So the interval
). So the interval ![[\sqrt{m}, \sqrt{2m}] [\sqrt{m}, \sqrt{2m}]](//s0.wp.com/latex.php?latex=%5B%5Csqrt%7Bm%7D%2C+%5Csqrt%7B2m%7D%5D&bg=ffffff&fg=000&s=0) is of length >2, which means that that it contains two distinct natural numbers
is of length >2, which means that that it contains two distinct natural numbers 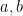 . Now:
. Now:
where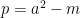 ,
, 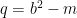 . Then
. Then 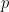 and
and 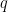 satisfy the requirements of the question.
satisfy the requirements of the question.
Lovely
So, the next question is, what other sufficient conditions for non-traceability might exist?